INTRODUCTION TO DISTRIBUTION THEORY

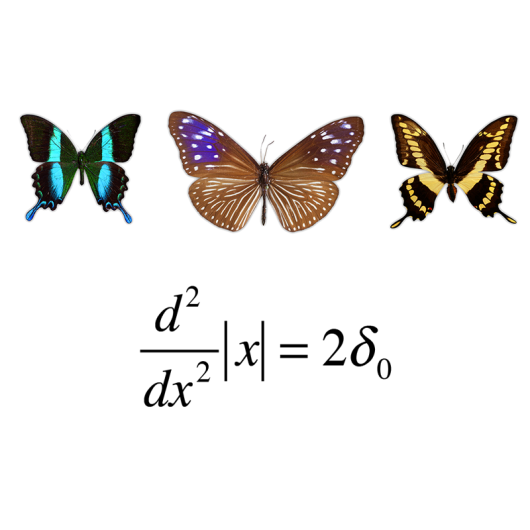
PRESENTATION:
Can a discontinuous function solve a differential equation? How can we strictly define Dirac mass (a “function” of integral one that is equal to zero everywhere except at one point) and its derivatives? Can we define the notion of a “fractional order derivative”? This introduction to distributions addresses these questions and many more.

ABOUT THE COURSE

In numerous scientific disciplines (physics, mechanics, numerical analysis etc.), there is a need to develop a “generic” differential calculus for irregular functions, for example discontinuous ones. The first lesson presents such a situation. The purpose of this course is to offer an introduction to distribution theory, which provides an elegant answer to this problem.
Firstly, we present the notion of distribution, and in doing so, genericize the notion of function, and we look at the initial properties of these mathematical objects. We then demonstrate how some well-known operations on functions, in particular derivation, can be naturally applied to the field of distributions. The course concludes with an introduction to some classic examples of linear partial differential equations.

COURSE SYLLABUS

Week 1 :
First-order PDEs and method of characteristics
Hopf equation
Test functions
Week 2 :
Definition of distributions
Derivation of distributions
Week 3 :
Other operations on distributions
Compact support distributions
Convolution of distributions by regular functions
Week 4 :
Formula of multi-dimensional jumps and applications
Compact support distributions
Convolution of distributions by regular functions
Week 5 :
Regularization of distributions
Convolution des distributions
Tempered distributions
Week 6 :
Fourier transform on the Schwartz class
Fourier transform for tempered distributions
Week 7 :
Introduction to the study of PDEs
Examples of elementary solutions
Determination of some elementary solutions
Week 8 :
Harmonic functions
Examples of elementary solutions
Poisson’s equation
Week 9 :
Cauchy problem in the context of distributions
Examples of first-order evolutionary partial differential equations
Example of a second-order evolutionary partial differential equation
REQUIREMENTS

Multivariable differential calculus
Basic notions of topology
Knowledge of the Lebesgue integral
FAQ

Is it possible to get a certificate upon completion of the course?
Yes. All students who follow the entire course and complete the final multiple-choice quiz will receive a certificate. However, this certificate does not entitle you to ECTS credits.

What do I need for this course?
You just need to watch the videos of the course to be able to benefit from it. Additional information can be downloaded if necessary.